Equations of Freedom (Money)

Foundations of Cryptography: Groups, Rings, and Finite Fields

Building Blocks of Secure Systems

To understand the cryptographic principles underpinning decentralized systems like Bitcoin and Monero, we begin with three mathematical pillars: groups, rings, and fields. These structures enable the privacy, security, and trustlessness of modern cryptocurrencies.

[NOTE: Written by DeepSeek R1. Still learning about this topic myself; these are my notes so far.]

1. Cryptographic Essentials: Groups, Rings, and Fields

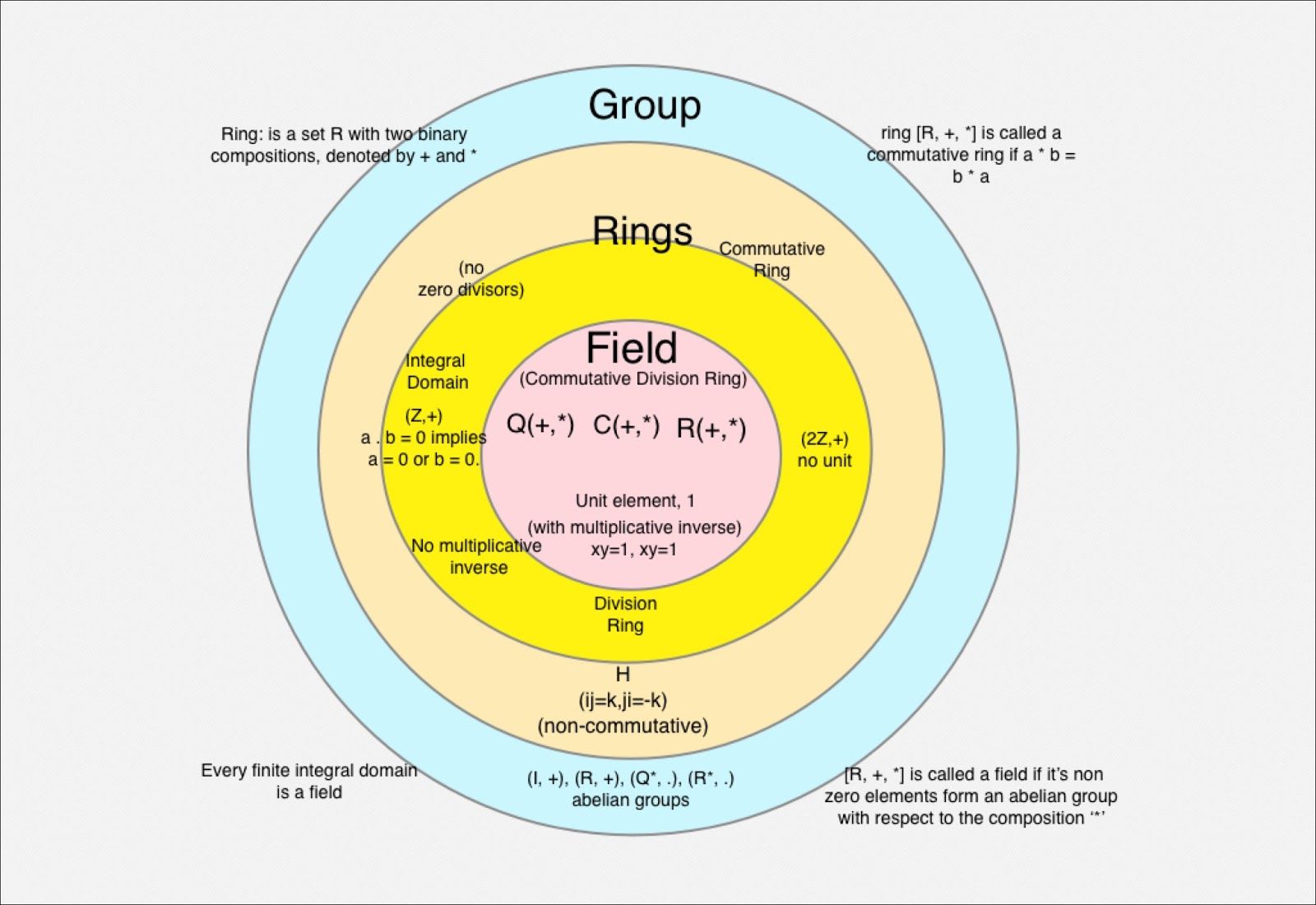
Groups: Operations with Structure

A group is a set G paired with an operation (e.g., addition, multiplication) satisfying:

• Closure: For all a, b ∈ G, the result of a · b stays in G.
• Associativity: a · (b · c) = (a · b) · c.
• Identity: An element e ∈ G exists such that a · e = e · a = a.
• Inverses: For every a ∈ G, there exists b ∈ G where a · b = e.

Examples:

• Integers ℤ under addition: Identity is 0; inverse of 5 is -5.
• Elliptic curve groups: The basis of Bitcoin’s ECDSA, where solving k · G = P (finding scalar k from public point P) is computationally infeasible.

Rings: Dual Operations

A ring adds a second operation to a group:

• Addition is commutative (abelian group).
• Multiplication is associative and distributive over addition.

Examples:

• Integers ℤ with addition and multiplication.
• Polynomial rings ℤ[x], crucial for constructing finite fields.

Fields: Division and Perfection

A field is a ring where every non-zero element has a multiplicative inverse. Key examples:

• Prime fields: Integers modulo a prime p (e.g., ℤ/7ℤ: 3⁻¹ = 5 in mod 7).
• Extension fields: Built by extending prime fields with irreducible polynomials (e.g., 𝔽₂⁸ used in AES).

2. Finite Fields: Cryptography’s Workhorse

Finite fields (Galois* fields) enable secure computation:

1. Prime fields: Arithmetic modulo p, like Bitcoin’s ℤ/pℤ for large primes.
2. Polynomial extensions: Construct 𝔽ₚⁿ by adjoining roots of irreducible polynomials.

Example: 𝔽₄

• Base field: 𝔽₂ = {0, 1}.
• Define 𝔽₄ = 𝔽₂[x]/(x² + x + 1). Elements: {0, 1, x, x+1}.
• x behaves like a root: x² ≡ x + 1 in this field.

3. Cryptography in Practice: Bitcoin and Monero

Bitcoin: ECDSA over Prime Fields

• Private keys: Integers k in ℤ/pℤ.
• Public keys: Points K = k · G on an elliptic curve (e.g., secp256k1).

Monero: Privacy Through Algebra

• Ring Signatures: Combine signatures using group operations.
• Stealth Addresses: Generate one-time keys via field arithmetic.

4. Sovereignty Through Mathematics

Bitcoin and Monero use openly verifiable structures:

1. Prime fields for collision-resistant hashing.
2. Elliptic curve groups for unforgeable signatures.
3. Polynomial rings for efficient zero-knowledge proofs.

Conclusion: Equations of Freedom

Groups (ℤ, elliptic curves), rings (ℤ[x]), and fields (𝔽ₚ) are tools of liberation. By encoding rights into mathematical protocols, Bitcoin and Monero shift power from intermediaries to individuals.

Trust math, not middlemen.

Notes

• * Évariste Galois, French mathematician. His last name is pronounced "Gal-wah" (/ɡalˈwa/ in IPA).

Sources

• DeepSeek R1 synthesis of its own training data plus the following additional sources:
• https://people.csail.mit.edu/madhu/ST12/scribe/lect03.pdf
• https://www-users.cse.umn.edu/~brubaker/docs/152/152groups.pdf
• https://people.maths.ox.ac.uk/flynn/genus2/sheets0405/grfnotes1011.pdf
• https://people.engr.tamu.edu/andreas-klappenecker/629/finite_fields.pdf
• https://www.geeksforgeeks.org/group-rings-and-fields-in-group-theory/

Inspired by: "Motivate The Math" Podcast, by Fundamentals and average_gary

• Motivate The Math: https://serve.podhome.fm/motivate-the-math_638723836566573210